Ich würde noch gerne anmerken, dass nicht jeder überwachte Algorithmus eine Klassifikation durchführen muss (vielleicht war das nicht so gemeint, aber es hat sich so gelesen). Die Outputs können auch Zahlen sein. Klassische Regression ist ja ein klassischer überwachter Algorithmus.

Machine Learning Algorithmen – der Schlüssel in die Welt der Daten
Daten, Daten, überall Daten – Banken verfügen über eine kontinuierlich wachsenden Menge an Kundendaten. Aber was tun mit diesem wertvollen „digitalen Gold“? Data Analytics Algorithmen, auch bekannt als Machine Learning Algorithmen, können der Schlüssel in eine neue Welt voller Erkenntnissen und Einblicken sein. Aber wie funktionieren die Algorithmen eigentlich? Mit der Frage setzte ich mich schon länger auseinander. In vorherigen Blogbeiträgen habe ich die unterschiedlichen Kategorien der Algorithmen erläutert, sowie neuronale Netze als Beispiel für einen überwachten (supervised) Algorithmus erklärt. Heute widme ich mich den Support Vector Machines, ebenso ein supervised Algorithmus, es geht also um eine Klassifizierung.
Angeommen wir haben Kundendaten mit 100 verschiedenen Variablen, z.B. Wohnort, Alter, Anzahl der Dauerüberweisungen, Gehaltshöhe, etc. und möchten nun vorhersagen, ob der Kunde seinen offenen Kredit pünktlich zurückzahlt (1) oder nicht (0). Aufgrund unserer historischen Daten, die bereits beinhalten, ob ein Kunde pünktlich zurückgezahlt hat, können wir unser Machine Learning Modell „trainieren“ (s. Blogbeitrag), um für zukünftige Kunden das oben genannte Szenario vorherzusagen. Ziel ist es also, die Objekte in zwei Klassen einzuteilen.
Stellen wir uns diese Daten nun in einem 100-dimensionalen Raum vor, jeder Punkt (Objekt) entspricht einem Kunden. Nun versuchen wir diese Objekte in zwei Klassen mit Hilfe einer Gerade zu teilen.
Funktioniert? Wie gut ist Ihre Vorstellungskraft? Ja, genau, hier ist das Problem. 100-dimensionaler Raum? Schwierig.
Und jetzt kommt der („Kernel“) Trick.
Anstatt sich mit komplizierten Formeln zu quälen, um eine 100-dimensionale Funktion durch die Objekte zu legen, lösen das SVM ganz geschickt. Und zwar übertragen sie die Objekte erst in ein 2- oder 3-dimensionalen Raum, um dann normale Algebra anzuwenden. So lassen sich die 2-dimensionalen neuen Objekte, welche repräsentativ für einen 100-dimensionalen Kunden stehen, einfacher in zwei Klassen teilen. Clever, oder?
Nun suchen SVM die Trennlinie (oder Hyperebene in einem 3-dimensionalen Raum) zwischen den beiden Klassen mit der größten Marge (s. Abbildung) zu den nahen liegenden Objekten (Support Vector genannt). In der Abbildung gehören die Sterne also einer Klasse an (Kunde zahlt Kredit zurück) und die Kreise der anderen Klasse.
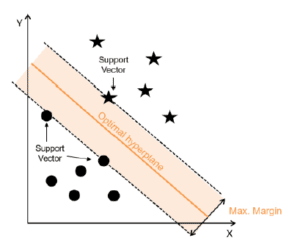
#COPYRIGHT#
Achtung – mathematisch! (überspringbar)
In dem Fall, dass keine lineare Trennlinie gefunden werden kann, wird noch ein Strafparameter eingeführt. Somit werden nahe liegende Objekte ignoriert oder falsch klassifizierte Objekte genehmigt, sodass die Marge größer wird. Ein hoher Strafparameter lässt keine falschen Klassierungen zu, wohingegen bei einem geringen Strafparameter, falsch klassierte Objekte ignoriert werden können, da die „Bestrafung“ nicht zu groß ist. Mit Hilfe des Strafparameters findet also ein Trade-off zwischen Over- und Underfitting statt. Die Abbildung unten verdeutlicht das Over- und Underfitting Problem, welches in bereits in einem vorherigen Blogbeitrag erläutert habe. Ist ein Model overfittet (rechts), passt es sich sehr genau den historischen Trainingsdaten an und ist somit schlechter wenn es zur Generalisierung kommt.
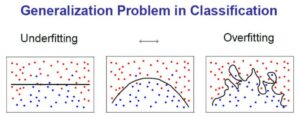
#COPYRIGHT#
Weitere Algorithmen, die tricksen.
Es gibt noch eine ganze Reihe von Algorithmen, die genau solch eine Transformation in ein 2- oder 3-dimensionalen Raum vornehmen. Dafür eignen sich unter anderem unüberwachte Machine Learning Algorithmen. Self-Organizing Maps (SOM) können hochdimensionale Inputdaten in geringere Dimensionen darstellen. SOMs sind eine Form von neuronalen Netzen, die ich bereits in einem vorherigen Beitrag erläutert habe.
Achtung – technisch! (überspringbar)
Eine SOM besteht aus einer vordefinierten Anzahl an Knoten („Nodes“). Dieses Netz passt sich nach und nach den originalen Inputdaten an. Für jedes Inputobjekt (also jedem Kunden) treten die Knoten sozusagen gegeneinander an, um zu schauen, wer dem Inputobjekt am ähnlichsten ist. Der „Gewinner“-Knoten rückt dem Inputobjekt dann ein Stück näher, um ein besseres Matching zukünftige Inputobjekte zu erreichen. Nicht nur der Gewinner, sondern auch dessen Nachbarn werden angepasst, allerdings weniger stark. So legt sich das Netz langsam um die Inputdaten herum (s. Abbildung).

#COPYRIGHT#
Als Output existiert nun also ein Netz mit repräsentativen Knoten, die eine geringere Dimension als die Inputobjekte haben, dessen Informationen aber bestmöglich innehalten. Diese Knoten lassen sich nun als Inputdaten für beispielsweise Segmentierungsalgorithmen verwenden.
Auch wenn sich diese Algorithmen kompliziert anhören, braucht es meist nicht mehr als 1-2 Zeilen Code, um diese umzusetzen. Nichtsdestotrotz finde ich es hilfreich sich mit der genauen Funktionsweise zu beschäftigen, um die Grenzen aber auch die Möglichkeiten der einzelnen Algorithmen zu verstehen. Denn nur so lässt sich aus den großen Mengen digitalen Gold wertvolles Wissen schaffen.
QUELLEN:
Alpaydin, E. (2014). Introduction to Machine Learning (Third edition). Adaptive com-putation and machine learning. Cambridge, MA: The MIT Press.
Christianini, N., & Schölkopf, B. (2002). Support Vector Machines and Kernel Meth-ods: The New Generation of Learning Machines. AI Magazine, 23(3).
Kohonen, T. (1998). The self-organizing map. Neurocomputing, 21(1-3), 1–6. https://doi.org/10.1016/S0925-2312(98)00030-7
Kohonen, T. (2013). Essentials of the self-organizing map. Neural Networks, 37, 52–65. https://doi.org/10.1016/j.neunet.2012.09.018
Kotsiantis, S. B., Zaharakis, I. D., & Pintelas, P. E. (2006). Machine learning: A review of classification and combining techniques. Artificial Intelligence Review, 26(3), 159–190. https://doi.org/10.1007/s10462-007-9052-3
Schufa, Creditreform etc. scheinen hier dann wohl einige Dekaden Vorsprung zu haben 😉
Hallo,
nach meinem Verständnis stimmt es nicht, dass SVMs die Daten nicht in einen zwei-oder drei-dimensionalen Raum übertragen. Vielmehr suchen sie eine Hyperebene (nicht zu verwechseln mit einer „Hyperbel“) um die Daten zu trennen. Bei einem drei-dimensionalen Datenraum (3 Features) wäre dies eine 2-dimensionle Fläche, bei vier Dimensionen ein 3-dimenaionales Objekt.
Viele Grüße
Moritz Bunse
Es ist eigentlich sogar andersrum. Bei SVMs werden die Dimensionen weiter aufgeblasen bis eine Hyperebene die Punkte trennen kann. Das ist nämlich umso schwieriger je weniger Dimensionen man hat.
Den Nachteil der hohen Dimensionalität umgeht man durch den Kernel, der den hochdimensionalen Raum in der niedrigen Dimension parametrisiert.
Die linear Trennung erfolgt allerdings im hochdimensionalen Raum. Normalerweise ist es also keine Gerade mehr wenn man auf 2D runterprojiziert, sondern eine allgemeine Kurve.
Hallo Moritz Bunse,
meines Wissens nach verwenden SVM einen Kernel, der das innere Produkt der einzelnen Punkte berechnet. Der Einfachheit halber habe ich es als Vereinfachung der Dimensionen bezeichnet.
Und vielen Dank für den Hinweis, bei „Hyperbel“ handelte es sich um einen unglücklichen Rechtschreib-/Denkfehler, den habe ich angepasst. Hyperbel ergibt in diesem Zusammenhang keinen Sinn!
Viele Grüße
Michelle Berger
Diese Themen interessieren uns
Learnings from ECB Exploratory Phase – Part 2: Review of the HTLC Mechanism
Learnings from ECB Exploratory Phase – Part 1


Luca Del Res (erster) Einwand ist richtig. Der Artikel scheint die Grundidee der SVM genau zu verdrehen.
Je höher die Dimension, desto einfacher ist es Eigenschaften mit einer „geraden“ (hyperebene) zu trennen. Wenn wir 100 verschiedene Kunden mit 100 Eigenschaften (= Dimensionen) haben, dann geht das immer. Diese Lösung ist aber nicht erstrebenswert, da sie höchstwahrscheinlich ein Overfitting darstellt. Man möchte die Eigenschaft auf wenige relevante Kenngrößen (= wenige Dimensionen) reduzieren.
Die Reduktion auf wenige Dimensionen ist also absolut keine Rechenvereinfachung, sondern eine Anforderung. Das Aufblähen auf viele Dimensionen ist eine Rechenvereinfachung, weil man hier sehr einfach eine lineare Trennung erreichen kann.
Man sucht nun im Niederdimensionenalen einen Trennung durch eine nicht-lineare function (also Hyperfläche statt Hyperebene) zu erreichen, in dem man die nicht-lineare niederdimensionale Hyperfläche durch eine lineare hochdimensionale Hyperebene beschreibt. Diese Transformation leistet der Kernel.
Diese Idee ist mathematisch nicht komplex und analog zur nicht-linearen Regression bei der man eine nicht-lineare Regressionsfunktion wie z = a * 1 + b * x + c * x^2 in einer Dimension x als eine lineare Regression z = a * 1 + b * x + c * y darstellt (mit den „Basisfunktionen“ x und x^2).
Bei der linearen Regression ist dann aber die ganze Kunst die Wahl der richtigen Basisfunktionen. Und diese Fragestellung existiert auch noch hier: was ist eigentlich ein guter Kernel? (Der Kernel ist nur das Skalarprodukt der Basisfunktionen). Dem Problem gute Basisfunktion zu wählen begegnet man z.B. bei der Bewertung von kündbaren Finanzprodukten. Probleme für deren Lösung die DZ BANK lange auch Experten hat (Grüße an Jan).